洪都拉斯进入紧急黄色预警状态,全天候警戒启动
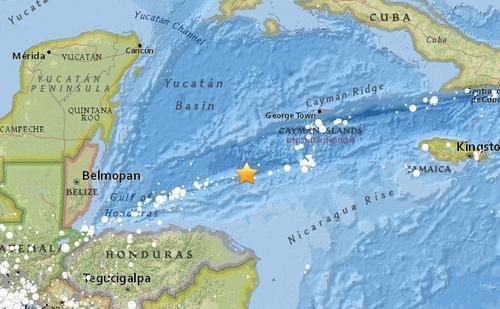
洪都拉斯进入为期24小时的黄色预警状态。目前,该国正面临某种紧急情况或潜在风险,需要保持高度警惕和准备应对可能出现的各种情况。预警状态的宣布是为了保障公民的安全和福祉,并尽量减少潜在风险的影响。具体情况尚待进一步公布...
北京警方刑拘买金女子案件,背后的深思与启示
北京警方刑拘一名买金女子,引发社会关注。此案件背后反映了当前社会一些不法分子利用黄金投资市场进行非法交易的问题。警方对此类行为采取严厉打击的态度,维护市场秩序和公众利益。此事件也提醒广大投资者要增强风险意识,遵守市场...
揭秘九寨沟景区关于免门票谣言,真相大揭秘!
九寨沟景区辟谣,澄清关于40岁以上游客免门票的传闻。真相是景区并未推出此类优惠政策。请游客们注意,九寨沟景区的门票价格仍然按照正常标准执行,没有年龄相关的优惠。游客在规划行程时,应关注官方渠道发布的信息,以免受到不实...
青春热血乒乓赞歌,王楚钦恭喜蒯曼的胜利
王楚钦祝贺蒯曼,青春热血在乒乓球场上奏响赞歌。两位年轻选手在比赛中展现出卓越实力和团队精神,用汗水和努力书写着青春的故事。这场激烈的比赛不仅是技术的较量,更是青春激情的碰撞。他们的表现,激励着更多年轻人为梦想拼搏,为...
丽江机场头等舱乘客登机牌遭撕事件引热议
丽江机场发生头等舱乘客登机牌被撕事件,引起社会广泛关注。该事件涉及到机场管理、服务质量以及乘客权益等多个方面,引发了公众对于机场管理漏洞和服务质量问题的热议。目前,事件的具体原因和后续处理尚待进一步披露。...
独立女性的力量与觉醒,国产剧中的女性崛起
国产剧中终于出现不再依赖男主拯救的女主角,展现了独立女性的力量与觉醒。这一进步凸显了女性自我成长和自主决策的重要性,挑战了传统性别角色设定。女性角色不再是被动等待救援的弱者,而是展现出坚韧、智慧和独立的精神面貌。这一...
中国冰雪热潮席卷全国
中国的冰雪运动热潮已经传遍大江南北,各地纷纷掀起冰雪运动的热潮。无论是城市还是乡村,人们都在积极参与冰雪活动,享受冰雪带来的乐趣。这一运动热潮不仅推动了冰雪产业的发展,也提高了人们的身体素质和健康水平。中国冰雪运动的...
揭秘哪吒的来源,是出自西游记还是封神榜?
哪吒的来源既可以是西游记也可以是封神榜。他是中国古代神话传说中的重要人物之一,关于其起源和传说有多个版本和流传。无论是西游记还是封神榜,都描绘了哪吒勇敢、正义的形象和身世故事。...
哪吒2,树中隐藏的人性深度剖析
摘要:在电影《哪吒2》中,场景中的树含人量过高,即树木中包含了过多的人类元素,影响了观众对自然与神话世界的感受。这一设计可能过于注重现实元素的融入,而忽略了神话本身所应有的奇幻色彩和超脱感。...
时代少年团与非洲,青春交响跨越文化与大陆界限
时代少年团与非洲文化交流,跨越文化与大陆的青春交响热烈上演。这支年轻乐团以音乐为桥梁,展现了青春活力与文化多样性。他们通过音乐传递中非友谊,展现了跨越大陆的青春力量和文化交融的美好前景。这次交流不仅是一次音乐的盛宴,...














 桂ICP备2021008493号-1
桂ICP备2021008493号-1